发表于

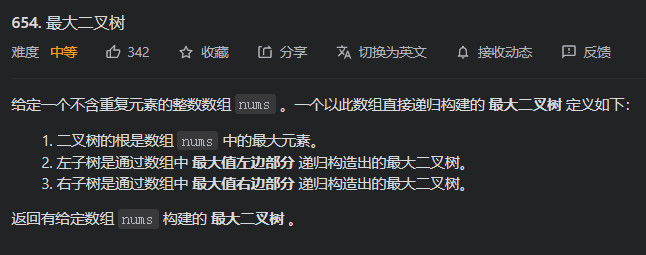
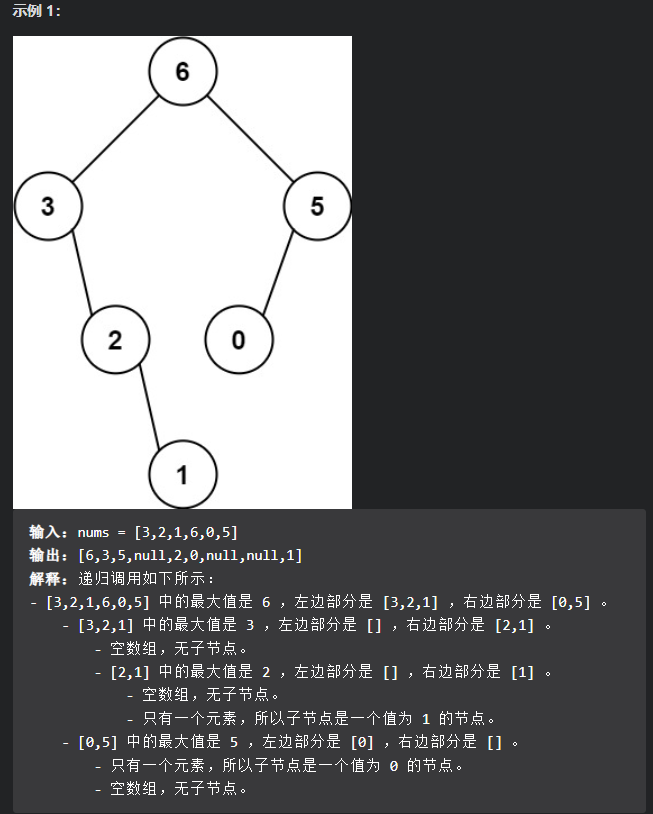
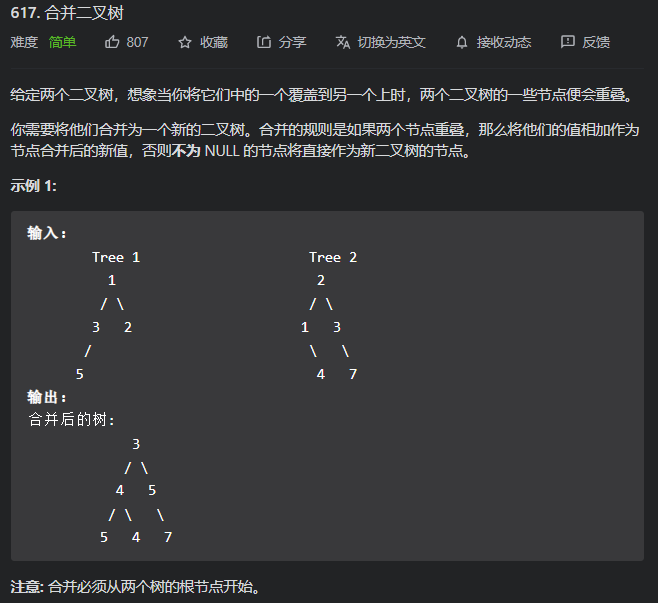
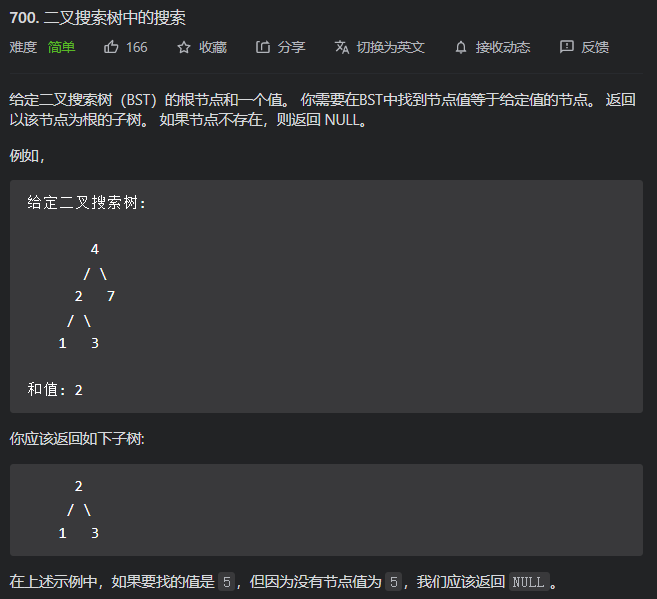
559. N 叉树的最大深度

题目

今天的lc每日一题

题目很简单，但是我猛然间将现在的代码和以前的代码做了一个对比，有了新发现

下面是我今天的代码，我的代码思路是每递归深入一层，就更新一次深度（初始深度为1），最后的全局变量就是答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int maxH;
    int maxDepth(Node* root) {
        if(root == nullptr) return 0;
        dfs(root, 1);
        return maxH;
    }

    void dfs(Node* root, int h){
        if(root == nullptr) return;
        if(maxH < h) maxH = h;
        for(int i = 0; i < root->children.size(); i++){
            dfs(root->children[i], h + 1);
        }        
    } 
};

这是我以前的代码，后序遍历，这就不是在求深度了，这是从底层往高层算，是在回溯，求的是高度，而二叉树的高度值与深度值大小相同，所以代码也就过了。

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    int maxDepth(Node* root) {
        if(root == nullptr) return 0;
        int max1 = 0;
        for(int i = 0; i < root->children.size(); i++) 
        max1 = max(max1, maxDepth(root->children[i]));
        return max1 + 1;
    }
};

这再次印证了Carl的话，递归和回溯的区别，一个去一个回，是截然不同的

发表于

236. 二叉树的最近公共祖先

题目

这个题直接g， 好久之前写的全忘了，方法太巧妙了

没做出来之前好难，看完了Carl的题解后，只想说两个点

返回值：这题居然是遍历整棵二叉树还附带返回值，在之前的题目中Carl的结论是【有返回值的递归是部分遍历】，这题发生了变化

回溯，自底向上。这道题拿到后很容易想到从底部向上移动，找出祖先节点。但这题给的条件是树的根节点，而且树是单向的，你没有第二个指针遍历回去，那怎么办呢？解决办法是回溯，既然有向下递归，那就有向上回溯，只要你进去了，总归是要出来的，然后向上返回就行了

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == p || root == q || root == NULL) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right, p, q);
        if(left != NULL && right != NULL) return root;
        else if(left == NULL && right != NULL) return right;
        else if(left != NULL && right == NULL) return left;
        else return NULL;

    }
};

594. 最长和谐子序列

每日一题

打卡题，不过还是被迷惑了一会

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    unordered_map<int, int> p;
    int findLHS(vector<int>& nums) {
        for(int i = 0; i < nums.size(); i++) p[nums[i]]++;
        int maxx = 0;
        for(auto& [x, cnt] : p) 
            if(p.count(x + 1))
            maxx = max(maxx, p[x] + p[x + 1]); 
        return maxx;
    }
};

235. 二叉搜索树的最近公共祖先

题目

这道题结合了二叉搜索树的性质，根据根节点的值决定递归遍历左子树或右子树

这题我只想说一点，部分遍历的问题

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root->val > p->val && root->val > q->val){
            TreeNode* left = lowestCommonAncestor(root->left, p, q);
            if(left) return left;
        }
        if(root->val < p->val && root->val < q->val) {
            TreeNode* right = lowestCommonAncestor(root->right, p, q);
            if(right) return right;
        }
        return root;
    }
};

701. 二叉搜索树中的插入操作

题目

基本的题目, 不过更高阶的做法写不出来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(root == nullptr) {
            TreeNode* node = new TreeNode(val);
            return node;
        }
        insert(root, val);
        return root;
    }

    void insert(TreeNode* root, int val){
        if(root->val > val){
            if(root->left == nullptr) {
                TreeNode* node = new TreeNode(val);
                root->left = node;
                return;
            }
            insert(root->left, val);
        } 
        if(root->val < val){
            if(root->right == nullptr) {
                TreeNode* node = new TreeNode(val);
                root->right = node;
                return;
            }
            insert(root->right, val);
        } 
    }
};

Carl的解法, 不愧是acm大神

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    TreeNode* insertIntoBST(TreeNode* root, int val) {
        if(root == nullptr){
            TreeNode* node = new TreeNode(val);
            return node;
        }
        if(root->val > val) root->left = insertIntoBST(root->left, val);
        if(root->val < val) root->right = insertIntoBST(root->right, val);
        return root;
    }
};

发表于

397. 整数替换

每日一题

简单的递归，注意值的边界问题

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int res = 0x3f3f3f3f;
    int integerReplacement(long long n) {
        if(n == 1) return 0;
        if(n & 1) {
            return 1 + min(integerReplacement(n - 1), integerReplacement(n + 1));
        }
        return 1 + integerReplacement(n / 2);
    }
};

530.⼆叉搜索树的最⼩绝对差

题目

很简单的题目,把握好中序遍历就行了,都是些小细节

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int ans = INT_MAX;
    TreeNode* node = NULL;
    int getMinimumDifference(TreeNode* root) {
        if(root->left) ans = getMinimumDifference(root->left);
        if(node != nullptr) ans = min(ans, root->val - node->val);
        node = root;
        if(root->right) ans = getMinimumDifference(root->right);
        return ans;
    }
};

501.⼆叉搜索树中的众数

题目

水题，先上自己的版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    unordered_map<int, int> p;
    int mi = -1;
    vector<int> vec;
    vector<int> findMode(TreeNode* root) {
        dfs(root);
        for(auto &[a, b] : p){
            if(mi == b) vec.push_back(a);
        }
        return vec;
    }

    void dfs(TreeNode* root){
        if(root == nullptr) return ;
        dfs(root->left);
        p[root->val]++;
        mi = max(p[root->val], mi);
        dfs(root->right);
    }
};

利用搜索二叉树的原理进行优化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//没啥说的,随便改改就好了
class Solution {
public:
    int mi = 1;
    vector<int> vec;
    vector<int> findMode(TreeNode* root) {
        dfs(root);
        return vec;
    }
    TreeNode* pre = NULL;
    int count = 1;
    void dfs(TreeNode* root){
        if(root == nullptr) return ;
        dfs(root->left);
        if(pre != NULL && pre->val == root->val) {
            count++;
            if(count > mi) {
                mi = count;
                vec.clear();
                vec.push_back(root->val);
            }
            else if(count == mi) vec.push_back(root->val);
        }
        else if(pre == nullptr || pre->val != root->val) {
            count = 1;
            if(count == mi) vec.push_back(root->val);
        }
        pre = root;
        dfs(root->right);
    }
};

二叉树所有的迭代法周目二再说！

发表于

563. 二叉树的坡度

没想清除一个点，被卡了好久，二叉树的遍历别看只有短短几行代码，递归起来是真的要命，不好debug就很麻烦了，准备后期放假了玩命刷，现在就尽量把每题精刷一遍

图片

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    int ans;
    int findTilt(TreeNode* root) {
        if(root == nullptr) return 0;
        dfs(root);
        return ans;
    }
    int dfs(TreeNode* root){
        //if(root->left == nullptr && root->right == nullptr) return root->val;
        int l = 0, r = 0;
        if(root->left) l = dfs(root->left);
        if(root->right) r = dfs(root->right);
        ans += abs(l - r);
        return l + r + root->val;
    }
};

没想清楚的是【递归返回值】，我错误地认为【返回值】能干同时干两件事：返回正确答案+能跑递归代码。实际上只能干一件事，就是跑代码。题目的答案则需要用一个ans另外计算

递归水太深，把握不住

654.最大二叉树

构建二叉树只会写模板题，还要加强练习

题目

题目

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        TreeNode* node = new TreeNode(0);
        if(nums.size() == 1){
            node->val = nums[0];
            return node;
        }

        int maxValue = 0, maxIndex = 0;
        for(int i = 0; i < nums.size(); i++){
            if(maxValue < nums[i]) {
                maxValue = nums[i];
                maxIndex = i;
            }
        }
        node->val = maxValue;
        //保证左边有一个节点
        if(maxIndex > 0){
            vector<int> newVec(nums.begin(), nums.begin() + maxIndex);
            node->left = constructMaximumBinaryTree(newVec);
        }
        //保证右边有一个节点
        if(maxIndex < (nums.size() - 1)){
            vector<int> newVec(nums.begin() + maxIndex + 1, nums.end());
            node->right = constructMaximumBinaryTree(newVec);
        }
        return node;
    }
};

简单暴力的写法，思路清晰，还学到一个技巧，动态数组还能这么玩

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return dfs(nums, 0, nums.size());
    }

    TreeNode* dfs(vector<int>& nums, int left, int right){
        //左闭右开区间
        if(left >= right) return nullptr;
        TreeNode* node = new TreeNode(0);
        int maxIndex = left;
        for(int i = left + 1; i < right; i++){
            if(nums[maxIndex] < nums[i]) {
                maxIndex = i;
            }
        }
        node->val = nums[maxIndex];
        //实际取值区间【left， maxIndex - 1】
        node->left = dfs(nums, left, maxIndex);
        //实际取值区间【maxIndex + 1， right - 1】
        node->right = dfs(nums, maxIndex + 1, right);
        //这样就把中间值maxIndex跳过去了
        return node;

    }
};

第二种方法把空节点引入到了递归中，所以省去了两个if条件

617. 合并二叉树

题目

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if(root1 == nullptr && root2 == nullptr) return NULL;
        if(root1 == nullptr || root2 == nullptr) return root2 == nullptr ? root1 : root2;
        root1->val += root2->val;
        root1->left = mergeTrees(root1->left, root2->left);
        root1->right = mergeTrees(root1->right, root2->right);
        return root1;
    }
};

将root2树上的值移到root1树上就行了

700. 二叉搜索树中的搜索

题目

白给题

递归法

1
2
3
4
5
6
7
8
9
10
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root == nullptr) return nullptr;
        if(root->val > val) return searchBST(root->left, val);
        if(root->val < val) return searchBST(root->right, val);
        return root;

    }
};

迭代法

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        while(root != NULL){
        	if(root->val > val) root = root->left;
        	else if(root->val < val) root = root->right;
        	else return root;
        }
        return NULL;
    }
};

98. 验证二叉搜索树

题目

踩陷阱啦，我憨憨地用递归直接进行判断，左边val小右边val大，然后直接gg

正确思路应该是用中序遍历把它输出成数组，然后在数组里面判断是否是严格递增序列，不是判false

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    vector<int> result;
    bool isValidBST(TreeNode* root) {
        dfs(root);
        if(judge(result)) return true;
        return false;
    }
    void dfs(TreeNode* root){
        if(root == nullptr) return;
        dfs(root->left);
        result.push_back(root->val);
        dfs(root->right);
    }
    bool judge(vector<int>& res){
        for(int i = 0; i < res.size() - 1; i++)
            if(res[i] >= res[i + 1]) return false;
        return true;
    }
};

今天就到这吧

发表于

题外话

不要学地理，会变得不幸！注册一个傻逼esri账户，各种给我报错，我的电脑一碰就错，同学的电脑一试就行，我真的杀人的心都有了，我弄了三节课一直报错（有心栽花），同学w在那边看漫画边弄（还是我指点的），一节课就弄好了（无心插柳）。最后下午还是用w的电脑弄好的。。地理信息真的是个傻逼专业，建议关了

318. 最大单词长度乘积

题目

这个题乍一看没思路，想清楚了其实很简单，就是一个位运算预处理，然后就是常规遍历。剩下的都是一些细节处理

如何快速检测两个单词有没有重复字母？答案是哈希化处理。创建一个26位的数字，记录每个字母是否在哈希表中出现过，如果出现则设为1，没有出现就是0，这样预处理万所有单词后，枚举所有的情况，如果有两个单词的哈希值“相与”，如果结果为0则证明满足要求

细节：lc对c++及其不友好，稍微没写严谨就报错，比如(int)(words[i].size() * words[j].size())这行代码，多加了两对括弧才能开始跑代码，真的恶心

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    int maxProduct(vector<string>& words) {
        vector<int> state;
        for(auto &word : words){
            int num = 0;
            for(auto &c : word){
                num |= 1 << (c - 'a');
            }
            state.push_back(num);
        }
        int res = 0;
        for(int i = 0; i < words.size(); i++){
            for(int j = i + 1; j < words.size(); j++){
                if((state[i] & state[j]) == 0) 
                    res = max(res, (int)(words[i].size() * words[j].size()));
            }
        }
        return res;
    }
};

珍爱生命，远离c++

再说一点题外话吧

学校的课程一点用都没有，纯纯的耽误时间，我有这些功夫，刷题八股文项目，拿一个200k的offer（秋招群里有两个二三本的人都拿到了，他们刷的题还没我多）轻轻松松，每天怀着上坟的心情上课，我还要写学校布置的作业，还要跟专业老师配合，还要听对开发毫无卵用的线代，概率论，写他们的作业，让他们侵占我的学习时间，我感觉我好伟大，顶着这么多debuff现在11点还在这写lc和博客，睡前还得听英语，明天早晨7点多起来继续还得的刷lc，看js。我越来越搞不懂我自己了吗？不，恰恰相反，我太清楚我这个时间点要做什么了，所以对未达标很痛苦 。我渴望有一天能活的纯粹一点

没啥说的了，生命不息，圣战（run）不止

发表于

113. 路径总和 II

题目

经过昨天的思考后，今天这题能直接秒了。仔细观察这个写法，我发现递归函数dfs每次都对函数进行了判断，判断这个

点是不是叶子节点，所以这对所有节点适用，但要记得此时的tar已经减去了这层的节点值了

关于特判，这个题只有主函数特判了初始的节点，后面如果再出现空节点函数dfs会忽略过去

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    vector<vector<int>> pathSum(TreeNode* root, int targetSum) {
        if(root == NULL) return result;
        path.push_back(root->val);
        dfs(root, targetSum - root->val);
        return result;
    }

    void dfs(TreeNode* root, int targetSum){
        if(root->left == NULL && root->right == NULL && targetSum == 0) {
            result.push_back(path);
            return ;
        }
        if(root->left){
            path.push_back(root->left->val);
            dfs(root->left, targetSum - root->left->val);
            path.pop_back();
        }
        if(root->right){
            path.push_back(root->right->val);
            dfs(root->right, targetSum - root->right->val);
            path.pop_back();

        }
    }
};

通过

106. 从中序与后序遍历序列构造二叉树

题目

这个已经一两个月没写了，忘完了，直接看题解吧 ^_^

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    unordered_map<int, int> p;
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int n = inorder.size();
        for(int i = 0; i < n; i++){
            p[inorder[i]] = i;
        }
        return dfs(inorder, postorder, 0, n - 1, 0, n - 1);
    }

    TreeNode* dfs(vector<int>& inorder, vector<int>& postorder, int il, int ir, int pl, int pr){
        if(pl > pr) return NULL;
        int key = postorder[pr];
        int k = p[key] - il;
        TreeNode* root = new TreeNode(key);
        root->left = dfs(inorder, postorder, il, il + k - 1, pl, pl + k - 1);
        root->right = dfs(inorder, postorder, il + k + 1, ir, pl + k, pr - 1);
        return root;
    }
};

用的y总的模板

难点1：边界处理，这里的边界是左闭右闭

难点2：后续遍历，在经过前几日的后序遍历的洗礼后，现在看后序遍历就有更新的体会了，这题用后序遍历特别巧妙的把一个问题划分为若干个子问题解决

再研究一下Carl的解法

我选择死亡，太多了。。。。。

不写啦

105. 从前序与中序遍历序列构造二叉树

题目

直接套用上一题的模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    unordered_map<int, int> pos;
    TreeNode* buildTree(vector<int>& pre, vector<int>& in) {
        int n = pre.size();
        for(int i = 0; i < n; i++) pos[in[i]] = i;
        return dfs(pre, in, 0, n - 1, 0, n - 1);
    }

    TreeNode* dfs(vector<int>& pre, vector<int>& in, int pl, int pr, int il, int ir){
        if(pl > pr) return NULL;
        int key = pre[pl];
        int k = pos[key] - il;
        TreeNode* root = new TreeNode(key);
        root->left = dfs(pre, in, pl + 1, pl + 1 + k - 1, il, il + k - 1);
        root->right = dfs(pre, in, pl + k + 1, pr, il + k + 1, ir);
        return root;
    }
};

五分钟搞定！

发表于

404. 左叶子之和

404. 左叶子之和

一个很简单的题目,我这里用dfs的遍历实现的，所以也就没有具体的遍历顺序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int ans = 0;
    int sumOfLeftLeaves(TreeNode* root) {
        dfs(root);
        return ans;
    }

    void dfs(TreeNode* root){
        if(root == nullptr) return;
        if(root->left) {
            if(root->left->left == nullptr && root->left->right == nullptr) 
                ans += root->left->val;
            dfs(root->left);
        }
        if(root->right) dfs(root->right);
    }
};

Carl的解法是标准的后序遍历方法，在了解了他的方法后我也仿写了一下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int sumOfLeftLeaves(TreeNode* root) {
        if(root == NULL) return 0;
        int left = sumOfLeftLeaves(root->left); //左
        int right = sumOfLeftLeaves(root->right);   //右
        //后序遍历法
        int sum = 0;
        if(root->left != NULL && root->left->left == NULL && root->left->right == NULL){
            sum = root->left->val;
        }//中
        return sum + left + right;
    }
};

时间复杂度O(n)，其中 n 是树中的节点个数。

空间复杂度O(n)，空间复杂度和深度优先搜索使用的栈内存有关，最坏情况下，树呈链式结构，深度为O(n),对应空间复杂度为O(n)

迭代法的实现

理论上来说能用递归的题目必然涉及到了栈， 那么就可以用迭代法模拟栈的运行写出题解，由于时间关系，这里就不说了，等下一轮复习的时候再刷一遍吧，我的想法是第一遍追求广度，第二遍后面追求深度！

513. 找树左下角的值

513. 找树左下角的值

拿到这个题第一反应是用bfs做，这种写法最简单，找到每一层第一个节点不断进行更新就可以了

bfs：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        queue<TreeNode*> q;
        q.push(root);
        int ans = root->val;
        while(q.size()){
            int size = q.size();
            for(int i = 0; i < size; i++){
                TreeNode* temp = q.front();
                q.pop();
                if(i == 0) ans = temp->val;
                if(temp->left) q.push(temp->left);
                if(temp->right) q.push(temp->right);
            }
        }
        return ans;
    }
};

再贴一个我的dfs解法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int maxH, ans;
    int findBottomLeftValue(TreeNode* root) {
        ans = root->val;
        dfs(root, 0);
        return ans;
    }
    void dfs(TreeNode* root, int depth){
        if(root == NULL) return ;
        if(maxH < depth) {
            ans = root->val;
            maxH = depth;
        }
        dfs(root->left, depth + 1);
        dfs(root->right, depth + 1);
    }
};

dfs的思路是不断地往左边找，每到最深一层就记录一下高度，最后就得到答案了

我感觉不是最优解，不太自信好像跟Carl的差不多，哈哈

112. 路径总和

路径综合

这个题目的测试点好恶心，故意卡边界，开局就两个边界给我干懵了。

对于根节点为空，直接返回false

对于根节点不为空，要特判整个树是否只有这一个节点并且等于target，返回true

处理完这两步后就可以写递归代码了，这题递归代码我采用了后序遍历，观察这个题你会发现，只要找出了一组答案，最终结果就是true了，这一点跟或（||）命令很像，只要有一个表达式为true满足了，整个表达式就为true。因此这里用后序遍历

在写完上面一段后，我突然发现有一个剪枝操作，如果有一个值为true，直接进入返回就好了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == NULL) return false;
            
        if(root->left == NULL && root->right == NULL && root->val == targetSum) 
            return true;
        return dfs(root->left, targetSum - root->val) || dfs(root->right, targetSum - root->val);
    }

    bool dfs(TreeNode* root, int targetSum){
        if(root == NULL) return false;
        if(root->left == NULL && root->right == NULL) {
            if(targetSum - root->val == 0) return true;
            else return false;
        }
        bool left = false, right = false;
        if(root->left) {
            left = dfs(root->left, targetSum - root->val);
            if(left) return true;	//剪枝，如果这一步执行了，后面的搜索就不用执行了
        }
        if(root->right) {
            right = dfs(root->right, targetSum - root->val);
            if(right) return true;	//后面的这个好像剪不掉了，为了整齐，还是加上吧
        }
        return left || right;
    }
};

剪枝

看了Carl的代码后感觉我太菜了，-_-，他的代码把边界情况处理的太好了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    bool hasPathSum(TreeNode* root, int targetSum) {
        if(root == NULL) return false;

        return dfs(root, targetSum - root->val);
    }

    bool dfs(TreeNode* root, int targetSum){
        if(!root->left && !root->right && targetSum == 0) return true;
        if(!root->left && !root->right) return false;

        if(root->left) 
            if(dfs(root->left, targetSum - root->left->val)) return true;
        if(root->right)
            if(dfs(root->right, targetSum - root->right->val)) return true;
        return false;
    }
};

我在写这个题目时遇到了一个问题就是把握不住tar减去val的时机，把整个过程都弄乱了，虽然最后勉强过了。。。。。

感觉没啥收获

反思

Carl的解法是先在开头特判了根节点，然后后面的代码就统一化了，就有点像是打印“1->2->3->4”这个字符串一样，先打印出“1”，后面每一步打印“->num”，这是做pat的常用套路。他这里的代码就是tar减去root->left->val，然后留在在下一层判断

我的解法就很乱了，我是在每一个结点都减去当前结点的值，然后进入递归函数进行判断，这样势必导致最后写递归出口的时候还要再减一次if（targetSum - root->val == 0）… 这么写太啰嗦了

把突然想到很重要的一点补上， 什么时候需要返回值？

Carl的说法是如果要搜索整个树，那就不要返回值。如果只是需要返回某一条路径，就需要返回值，遇到了符合条件的路径就返回。有了这个结论，以后再写递归就不会眉毛胡子一把抓了。

发表于

不想学习

不想学习，完全不想学习，上了一天的课已经不想去思考了，周六学了一天，周日学了一天，零零七也莫过于此了吧。我现在只想发呆 发呆 发呆，lc明天再更新吧

剩下的时间不多了

这个月还有一半，下个月是开始月，然后今年结束，一二月真的来的及准备春招吗，事情太多时间太少，我还是不够平静，随便吧，不要打乱自己的节奏

接下来

【计算机网络】，【lc】，【 js】， 【css】拿命肝吧，

“化鬼成魔，在所不惜” —– 《半泽直树》

发表于

257. ⼆叉树的所有路径

这个题出的好呀，一个简单题让我吃尽苦头

257

先说遍历，感觉用不了广搜，只能深搜，而且深搜还得用先序遍历

先序遍历的原因：先序遍历的顺序是“中左右”，这题我把“中”当做递归出口，而“左右”当做递归入口，只有在经历了大量搜索之后，然后判断已经到叶结点了，我就保存结果，执行return，递归结束

这个题难住我的一个地方之一就是回溯，根据Carl的理论，有递归式就必须有回溯式，递归和回溯永远是在一起的。对于回溯我的理解就是恢复现场

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    vector<string> result;
    vector<int> path;
    vector<string> binaryTreePaths(TreeNode* root) {
        dfs(root);
        return result;
    }
    void dfs(TreeNode* root){
        path.push_back(root->val);
        if(root->left == nullptr && root->right == nullptr) {
            string s;
            s += to_string(path[0]);
            for(int i = 1; i < path.size(); i++){
                s += "->";
                s += to_string(path[i]);
            }
            result.push_back(s);
            return ;
        }
        if(root->left) {
            dfs(root->left);
            path.pop_back();
        }
        if(root->right){
            dfs(root->right);
            path.pop_back();
        }
    }
};

剩下的没啥说的了，都是常规操作

100. 相同的树

待更新

101. 对称⼆叉树

待更新

发表于

222. 完全二叉树的节点个数

problem_1

对于这个题目，一开始很容易想到遍历，不管是前、中、后、层序遍历都是可以的遍历完一边后答案就出来了，太简单就不写了。说一下一个进阶的写法

转载了Carl哥的图

对于每一个棵树，首先就判断它整体是不是完全二叉树

如果是，那就很简单了，直接返回它的2^h即可，（h是高度，这个公式利用了满二叉树的性质）

如果不是，那么必然有一边是满二叉树，另一边不是满二叉树，那么就把这个问题细分为两个子问题再递归计算，这个问题会无限被细分成满二叉树，然后就可以套公式计算了，具体的操作步骤如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int countNodes(TreeNode* root) {
        if(root == nullptr) return 0;
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        int leftHeight = 0, rightHeight = 0;
        while(left){
            leftHeight++;
            left = left->left;
        }
        while(right){
            rightHeight++;
            right = right->right;
        }
        if(leftHeight == rightHeight) return (2 << leftHeight) - 1;
        else return countNodes(root->left) + countNodes(root->right) + 1; 

    }
};

110.平衡⼆叉树

image-20211113164842028

为什么要后序遍历?

因为要从根节点计算两边子树的高度，相减的结果就是判断返回值的依据

为什么返回-1

因为如果两棵子树的差大于1的话，那么他就不是平衡二叉树了，所以再返回高度就没有意义了，这时要返回一个绝对不可能出现的值标记失败（相当于返回值int承担了两个作用）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        return dfs(root) == -1 ? false : true;
    }

    int dfs(TreeNode* root){
        if(root == nullptr) return 0;

        int left = dfs(root->left);
        if(left == -1) return -1;
        int right = dfs(root->right);
        if(right == -1) return -1;
        if(abs(left - right) > 1) return -1;
        else return max(left, right) + 1;
    }
};

时间复杂度：O(n)

空间复杂度：O(n)

这道题一开始写还没写出来，连暴力法都没想出来，还要强加练习呀

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    bool isBalanced(TreeNode* root) {
        if(root == nullptr) return true;
        return abs(dfs(root->left) - dfs(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
    }

    int dfs(TreeNode* root){
        if(root == nullptr) return 0;
        return max(dfs(root->left), dfs(root->right)) + 1;
    }
};

暴力法

时间复杂度O(nlog(n))

空间复杂度O(n)