lc-day16

发表于 2021-11-28

每日一题 & js练习

438. 找到字符串中所有字母异位词

var findAnagrams = function(s, p) {
    const sLen = s.length, pLen = p.length;
    if(sLen < pLen) return [];

    const ans = [];
    const sCount = new Array(26).fill(0);
    const pCount = new Array(26).fill(0);
    for(let i = 0; i < pLen; i++){
        ++sCount[s[i].charCodeAt() - 'a'.charCodeAt()];
        ++pCount[p[i].charCodeAt() - 'a'.charCodeAt()];
    }
    if(sCount.toString() === pCount.toString()){
        ans.push(0);
    }
    for(let i = 0; i < sLen - pLen; i++){
        --sCount[s[i].charCodeAt() - 'a'.charCodeAt()];
        ++sCount[s[i + pLen].charCodeAt() - 'a'.charCodeAt()];
        if(sCount.toString() == pCount.toString()) ans.push(i + 1);
    }
    return ans;

};

蓝桥杯02

发表于 2021-11-28

激光炸弹

还卡我内存，一时代码还没过

学到了两个前缀和的运用技巧

关于初始化数组：可以将所有坐标+1，这样就回避了边界问题

前缀和问题可以节省一个数组，内存开销变小

边长r = x2 - x1 + 1, 如果题目给的是坐标, 那就是 x1 - 1 = x2 - r, 因为坐标x1是包括进矩形的,所以从x1 - 1开始,但这样也带来了一个问题, x1不能为0, 所以数组要从1开始计数

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N = 5010;
int s[N][N];
int n, r;

int main(){
    cin >> n >> r;
    r = min(r, 5001);
    for(int i = 0; i < n; i++){
        int x, y, w;
        cin >> x >> y >> w;
        s[++x][++y] += w;
    }
    for(int i = 1; i <= 5001; i++){
        for(int j = 1; j <= 5001; j++){
            s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
        }
    }
    int res = 0;
    for(int i = r; i <= 5001; i++){
        for(int j = r; j <= 5001; j++){
            res = max(res, s[i][j] - s[i - r][j] - s[i][j - r] + s[i - r][j - r]);
        }
    }
    cout << res << endl;
    
    return 0;
}

K倍区间

这题的方法太妙了，首先前缀和就不说了，直接上公式， s[R] - s[L - 1] % k == 0 ==> s[R] % k == s[L - 1] % k ，所以只要有两个数s[R] 和 s[L - 1]的前缀和mod k的余数相同，那么就必然是一个K倍区间，所以每次出现一个之前出现过的mod k的余数的数，就要res += cnt[之前出现过的余数]，而且还要出现次数加一

最后是一个边界问题，因为上面的都是两个端点所组成的区间（不包括左端点，所以是2~n的所有序列和子序列被包括了），有一种情况被排除了==>[0, n]，所以一开始就要包括cnt[0]=1, 这个区间的第一个值为零，所以是一个万能区间（因为值为0，对余数无影响），只要有[1, n]的数符合情况，那它也就非零了

#include<iostream>
using namespace std;

const int N = 1e7 + 10;
int s[N], cnt[N];
int n, k;
int main(){
    cin >> n >>k;
    long long ans = 0;
    //cnt[0] = 1;
    for(int i = 1; i <= n ; i++){
        
        cin >> s[i];
        s[i] = (s[i - 1] + s[i]) % k;
        ans += cnt[s[i]];
        cnt[s[i]] ++;
    }
    cout << ans + cnt[0]<< endl; 
    
    return 0;
}

数的三次方根

简单地二分

#include<iostream>
using namespace std;

int main(){
    double a;
    scanf("%lf", &a);
    double l = -10000, r = 10000; 
    while(r - l > 1e-8){
    	double mid = (r + l) / 2;
    	if(mid * mid * mid >= a) r = mid;
    	else l = mid;
    	printf("%lf\n", mid);
	}
	printf("%lf\n", l);
	return 0;
}

蓝桥杯01

发表于 2021-11-27

机器人跳跃问题

把二分复习了一遍

#include<iostream>
#include<vector>
using namespace std;
const int N = 100010;
int a[N];
int n;
bool check(int e){
    for(int i = 0; i < n; i++) {
        e = 2 * e - a[i];
        if(e >= 1e5) return true;
        else if(e < 0) return false;
    }
    return true;
}

int main(){
    cin >> n;
    for(int i = 0; i < n; i++){
        scanf("%d", &a[i]);
    }
    int l = 0, r = 1e5;
    while(l < r){
        int mid = (l + r) >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }
    cout << l << endl;
    return 0;
}

二分题，不过要考虑许多边界问题

子矩阵的和

#include<iostream>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], s[N][N];
int n, m, x;

int main(){
    cin >> n >> m >> x;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            cin >> a[i][j];
            s[i][j] = a[i][j] + s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
        }
    }
    while(x--){
        int x1, x2, y1, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        cout << s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] << endl;
    }
}

前缀和模板题

四平方和

先上一个tle的解法， O(n^2)超时

#include<iostream>
#include<vector>
#include<unordered_map>
using namespace std;
int n;
unordered_map<int, pair<int, int>> p;

int main(){
    
    cin >> n;
    for(int c = 0; c * c <= n; c++){
        for(int d = c; c * c + d * d <= n; d++){
            int t = c * c + d * d;
            if(p.count(t) == 0) p[t] = {c, d};
        }
    }
    
    for(int a = 0; a * a <= n; a++){
        for(int b = 0; b * b + a * a <= n; b++){
            int t = n - b * b + a * a;
            if(p.count(t)) {
                cout << a << " " << b << " " << p[t].first << " " << p[t].second;
                return 0;
            }
        }
    }
    
    return 0;
}

找了个能过的代码改了一下，二分法确实牛b

#include<iostream>
#include<vector>
#include<unordered_map>
#include<cmath>
#include<algorithm>
using namespace std;
const int N = 2500010;
int n;
struct Sum{
    int s, c, d;
    bool operator < (const Sum &t)const{
        if(s != t.s) return s < t.s;
        if(c != t.c) return c < t.c;
        return d < t.d;
    }
}sum[N];

int main(){
    int m = 0;
    cin >> n;
    for(int c = 0; c * c <= n; c++){
        for(int d = c; c * c + d * d <= n; d++){
            int t = c * c + d * d;
            sum[m++] = {t, c, d};
        }
    }
    sort(sum, sum + m);
    for(int a = 0; a * a <= n; a++){
        for(int b = 0; b * b + a * a <= n; b++){
            int t = n - b * b - a * a;
            int l = 0, r = m - 1;
            while(l < r){
                int mid = (l + r) >> 1;
                if(sum[mid].s >= t) r = mid;
                else l = mid + 1;
            }
            if(sum[l].s == t){
                cout << a << ' ' << b << ' ' << sum[l].c << ' ' << sum[l].d << endl;
                return 0;
            }
        }
    }
    
    return 0;
}

分巧克力

对区间数进行二分查找，时间复杂度为O（nlog（n））

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10;
int h[N], w[N];
int n, k;

bool check(int mid){
    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        res += (h[i] / mid) * (w[i] / mid);
        if (res >= k) return true;
    }
    return false;
}
int main(){
    
    cin >> n >> k;
    for(int i = 0; i < n ;i++){
        cin >> h[i] >> w[i];
    }
    int l = 0, r = 1e5;
    while(l < r){
        int mid = l + r + 1 >> 1;
        if(check(mid)) l = mid;
        else r = mid - 1;
    }
    cout << r << endl;
    return 0;
}

lc-day15

发表于 2021-11-27

860. 柠檬水找零

难题不会写，只能写简单题过日子这样子

空间还能优化一下，不想改了

class Solution {
public:
    bool lemonadeChange(vector<int>& bills) {
        unordered_map<int, int> p;
        for(int i = 0; i < bills.size(); i++){
            if(bills[i] == 5) p[5]++;
            if(bills[i] == 10) {
                if(p[5] == 0) return false;
                p[5]--;
                p[10]++;
            }
            if(bills[i] == 20){
                if(p[10] > 0){
                    if(p[5] > 0){
                        p[10]--;
                        p[5]--; 
                    }
                    else return false;
                }
                else if(p[5] > 2) {
                    p[5]--;
                    p[5]--;
                    p[5]--;
                }
                else return false;
            }
        }
        return true;
    }
};

星期六果然还是懒了, 今天就更新计网算了, 顺便打一下蓝桥杯的题目, LeetCode就一题吧

计算机网络笔记01

发表于 2021-11-26

前言

万众期待的计算机网络它来了，接下来我决定每天都更新一点计算机网络的学习笔记，这种方式能够加强自身的的学习印象~~（其实我写博客是为了面试加分）~~

看了个培训班的社招面试准备，给我整自闭了，项目多得跟喝汤一样，我真的有点怀疑人生了

第一章计算机网络和因特网

1.1 什么是因特网

我们可以从两个角度来回答这个问题：一种是描述组成它的软硬件；另一种是将其视为为分布式应用提供基础服务的联网设施来描述。其实，第一种角度，是从它的组成来描述，第二种角度是从它的功能来描述

1.1.1 组成描述

因特网是一个世界范围的计算机网络，这意味着它互联了数以亿计的计算设备（不仅仅是计算机哦）；这些设备包括但不限于传统PC、工作站以及所谓的服务器。现在有更多的设备加入到因特网中，比如便携式计算机、电视机、汽车、传感器等。用因特网的术语来说，所有连入因特网的设备都叫做主机或者端系统

端系统通过通信链路和分组交换机连接到一起。

分组交换机从它的一条入链路接收分组，并且选择一条出链路将分组转发出去；分组交换机也有很多种类，最为有名的是路由器和链路层交换机；两者的的不同之处在于，链路层交换机主要用在接入网中，路由器主要用在网络核心.

端系统通过因特网服务提供商（Internet Service Provider，简称ISP）接入因特网

很有名的协议有：**TCP（Transport Control Protocol，传输控制协议）和IP(Internet Protocol，网际协议)**；

服务描述

应用程序编程接口（API，Application Programming Interface)

1.1.3 协议

协议:定义了两个或多个通信实体（不一定是端系统，还有可能是分组交换机等）之间交换信息的格式和次序以及对该信息所采取的动作

1.2 网络的边缘

端系统：与因特网相连的计算机和其它设备，往往处于网络的边缘

端系统分类：客户和服务器

1.2.1 接入网

接入网：是指将端系统连入到边缘路由器的物理链路

边缘路由器：是指端系统到任何其他远程端系统路径上的第一台路由器

1.2.2 物理媒体

传输媒体是构成通信链路的主要部分，物理媒体通常可以分为导引性媒体和非导引性媒体；其中导引性媒体，信号沿着固体前行；而非导引性媒体中，信号沿着固体媒体前行

值得注意的是，架设传输媒体的人历成本要远远高于物理材料的成本

1.3 网络核心

网络核心即为由互联端系统的分组交换机和链路构成的网状网络

通过网络链路和交换机移动数据有两种基本方法：电路交换和分组交换

1.3.1 分组交换

分组在通信链路上以等于该链路的最大传输速率传输通过通信链路。因此如果某条链路的最大传输速率为R，分组长度为L，则该链路传输该分组的时间为L/R；这个时间也被称为传播时延

1.3.2 电路交换

在电路交换网络中，在端系统通信会话期间，交换机会预留端系统间通信路径上的相关资源（缓存，链路传输速率），即先建立连接，然后通信；而在分组交换网络中，这些资源没有被预留；也就是说，在端系统进行通信时，其所需要的资源是被保持的，其他通信是无法使用这一部分资源的；也就说，端系统间真正建立了一条“连接”；而这一连接，用电话的术语被称为“电路”。传统的电话网络就是电路交换网络的例子。

lc-day14

发表于 2021-11-26

45 跳跃游戏2

我好蠢，我好蠢，我好蠢，我好蠢，我好蠢，我好蠢，我好蠢，我好蠢，我好蠢…………

别人的更新方式各种ac，我的各种卡死

写了好久，最后还是看题解了

class Solution {
public:
    int jump(vector<int>& nums) {
        int start = 0, end = 1;
        int ans = 0;
        int maxPos = 0;
        while(end < nums.size()){
            for(int j = start; j < end; j++){	//左闭右开区间， 循环体更新maxpos
                maxPos = max(maxPos, j + nums[j]);
            }
            start = end;			//更新区间左右端点
            end = maxPos + 1;
            ans++;
        }
        return ans;
    }
};

这个作者的代码，严格遵循了左闭右开的习惯，在第二层循环中遍历完区间，然后更新左右端点

ver2.0

这个代码的优化版本 tql

class Solution {
public:
    int jump(vector<int>& nums) {
        int ans = 0;
        int end = 0;
        int maxpos = 0;
        for(int i = 0; i < nums.size() - 1; i++){
            maxpos = max(maxpos, i + nums[i]);
            if(end == i){	// 遇到当前覆盖的最远距离下标
                ans++;			//步数加1
                end = maxpos;	// 更新覆盖最远距离的下标
            }
        }
        return ans;
    }
};

1005. K 次取反后最大化的数组和

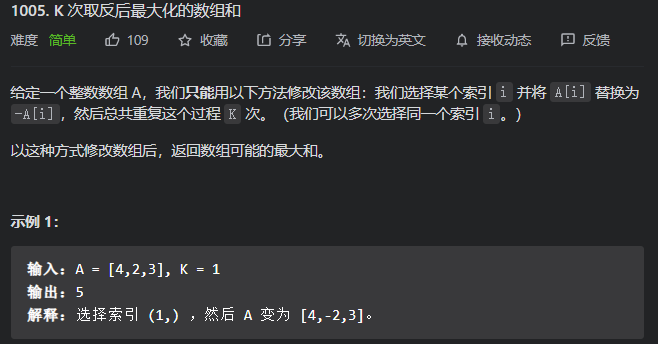
写了这么多题目，感觉还是啥也不会，想到了第一层，没想到第二层，想到了排序没想到取绝对值，想到了第一层没想到第二层，题目还是做少了，我是sb

class Solution {
public:
    static bool cmp(int a, int b){
        return abs(a) < abs(b);
    }
    int largestSumAfterKNegations(vector<int>& nums, int k) {
        sort(nums.begin(), nums.end(), cmp);
        for(int i = nums.size() - 1; i >= 0; i--){		//第一步局部最优， 负数取反
            if(nums[i] < 0 && k > 0) {
                k--;
                nums[i] = -nums[i];
            }
        }
        if(k % 2 == 1) nums[0] = -nums[0];		// 如果负数用完了，就判断k的奇偶性，判断是否要给绝对值最小的
        									//数取反
        int ans = 0;
        for(int &i : nums) ans += i;
        return ans;
    }
};

134. 加油站

class Solution {
public:
    int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {
        int rest = 0;
        int total = 0;
        int start = 0; 
        for(int i = 0; i < gas.size(); i++){
            rest += gas[i] - cost[i];
            total += gas[i] - cost[i];
            if(rest < 0) {
                start = i + 1;
                rest = 0;
            }
        }
        if(total < 0) return -1;
        return start;
    }
};

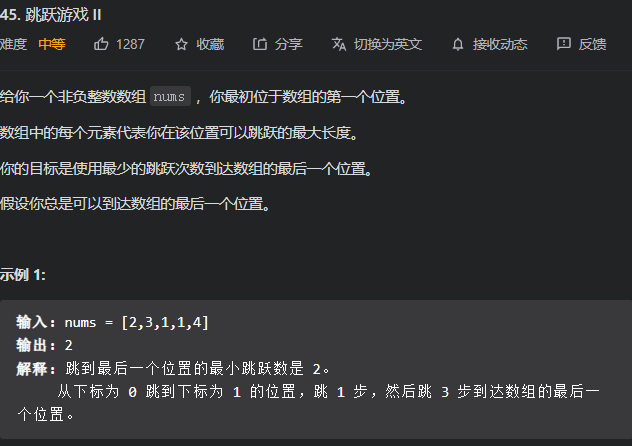
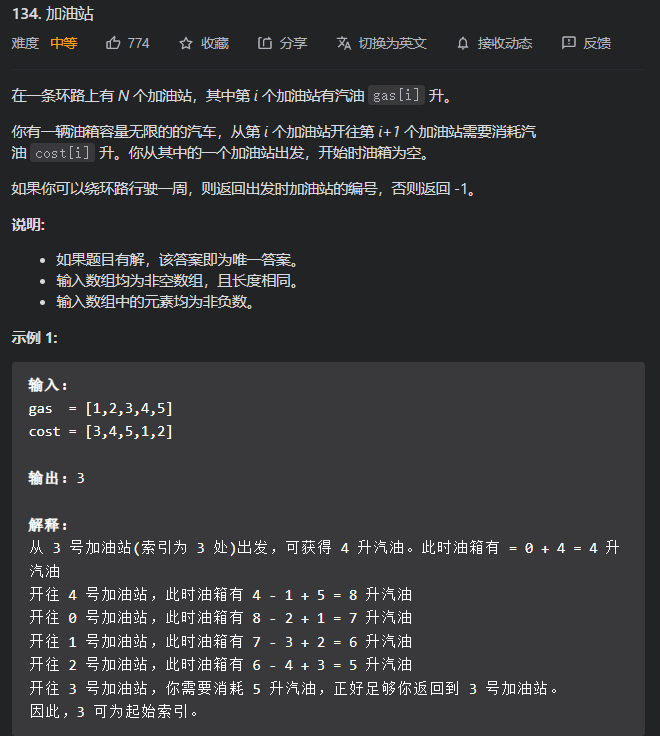
总结：如果x到不了y+1（但能到y），那么从x到y的任一点出发都不可能到达y+1。因为从其中任一点出发的话，相当于从0开始加油，而如果从x出发到该点则不一定是从0开始加油，可能还有剩余的油。既然不从0开始都到不了y+1，那么从0开始就更不可能到达y+1了…

lc-day13

发表于 2021-11-25

376. 摆动序列

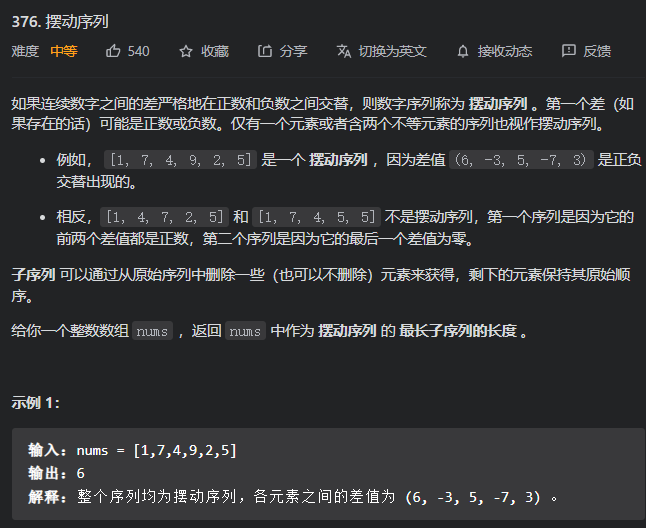
卡了一上午

贪心题还是挺麻烦的，至少我知道方法，但是没写出来（用Carl的话说就是：知道题目方法是常识性的东西，但是代码实现困难）

贪心主要方法：手动模拟方法，感觉可行，就试一试

难点1：如何设置寻找差值

有n个数，但是差值只有n-1个，怎么找呢。解决办法是在首部设置一个跟nums[0]相等的虚拟的数，然后就可以从第1个数开始算差值进行比较

class Solution {
    public int wiggleMaxLength(int[] nums) {

        // 先把结果值+1，因为 n 个数最多形成n - 1 个峰值。
        // 我们的解题逻辑 -> 峰值就是结果
        int result = 1;

        // 假设数组前有一个假元素。值等于数组第一个元素
        // preDiff = (nums[0] - nums[-1]) = 0
        int preDiff = 0;
        int curDiff = 0; 

        for(int i = 1; i < nums.length; i++){
            curDiff = nums[i] - nums[i -1];
            //如果当前差值和上一个差值为一正一负
            // preDiff = 0 是初始状态。
            // curDiff 为 0 时（前后元素相同），不进入if
            if((curDiff > 0 && preDiff <= 0) || (preDiff >= 0 && curDiff < 0)){
                result++;
                preDiff = curDiff;
            }
        }

        return result;
    }
}

难点2：为什么是prediff <= 0? 这个问题我认为应该分开来思考成两种情况，< 0就不说了，一正一负很好理解。

问题是为什么等于零？为什么cur 不等于0，pre可以等于0？题目不是要求一正一负吗？这个问题应该这样思考，pre为0，cur不为零，那么证明此时cur这个点是峰值（低谷）的。反过来，如果cur==0， pre != 0，那就是说当前元素cur跟前一个元素重复了，所以就不对了，这个解法中的pre只会在开始为0，后面pre的取值由cur更新，而cur == 0是不满足if条件的。换句话说，如果数组中有重复元素，它只会取第一个，这也是这个算法的巧妙性

还有一个y总的代码也挺好的，下次更新吧

53. 最大子序和

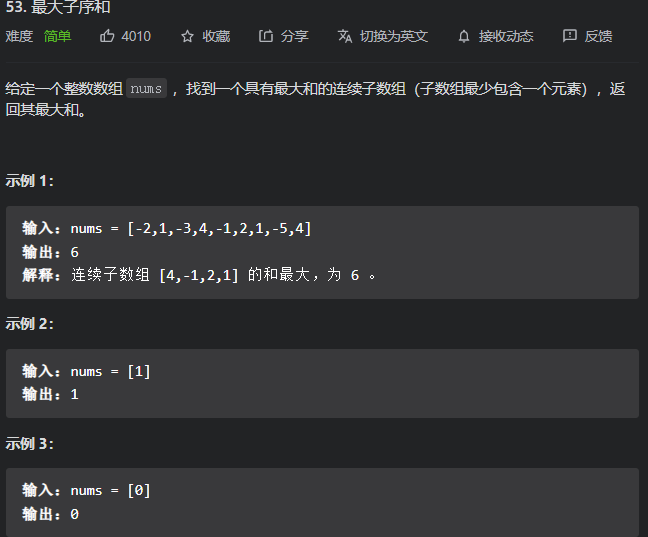
贪心解法

每次求值都进行选择,是当前的值【num[i]】更好还是【sum+num[i]】更好，局部最优形成全局最优

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int sum = 0, ans = -0x3f3f3f3f;
        for(int i = 0; i < nums.size(); i++){
            if(sum + nums[i] >= nums[i]) sum = sum + nums[i];
            else sum = nums[i];
            ans = max(ans, sum);
        }
        return ans;
    }
};

动态规划

核心公式差不多

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        if(nums.size() == 1) return nums[0];
        int ans = nums[0];
        int n = nums.size();
        int f[nums.size()];
        f[0] = nums[0];
        for(int i = 1; i < nums.size(); i++){
            if(f[i - 1] + nums[i] >= nums[i]) f[i] = f[i - 1] + nums[i];
            else f[i] = nums[i];
            ans = max(ans, f[i]);
        }
        return ans;
    }
};

122. 买卖股票的最佳时机 II

这题有一个误区，就是我能不能在同一天卖，然后再买。题目没说，那就应该是可以的。所以贪心的思路也就出来了，检查每两天的股票差值，是正值就买入，是负值就跳过，从局部最优到全局最优

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int ans = 0;
        for(int i = 0, j = 1; j < prices.size(); i++, j++){
            int pro = prices[j] - prices[i];
            ans = max(ans + pro, ans);
        }
        return ans;
    }
};

55. 跳跃游戏

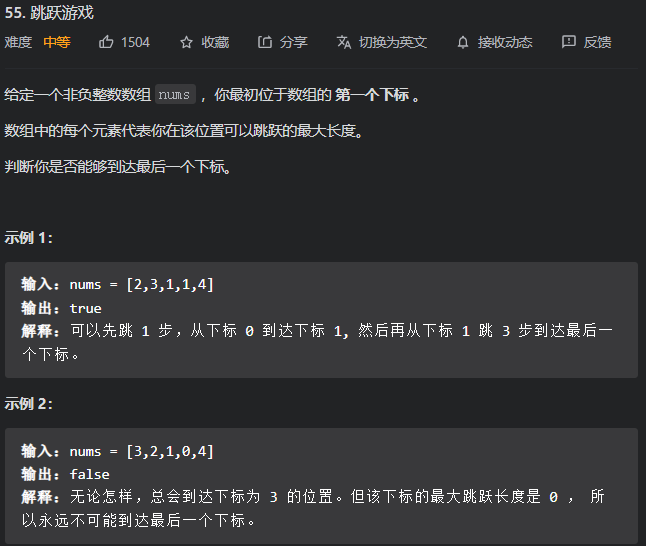
贪心题就是难想出来，代码其实挺简单的，这种题最重要的锻炼贪心思维

具体来说就是判断最大覆盖范围，如果在覆盖范围内就更新maxStep，最后结果就出来了

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int maxStep = 0;
        for(int i = 0; i < nums.size() - 1; i++){
            if(maxStep >= i) maxStep = max(maxStep, i + nums[i]);
        }
        
        if(maxStep >= nums.size() - 1) return true;
        return false;
    }
};

结尾

今天终于提起刷题的欲望了，但都是简单题？麻了，学计网去，等书到了开始更新计网的笔记，这种纯理论的东西就是记着玩，就是玩。

lc-day12

发表于 2021-11-24

455. 分发饼干

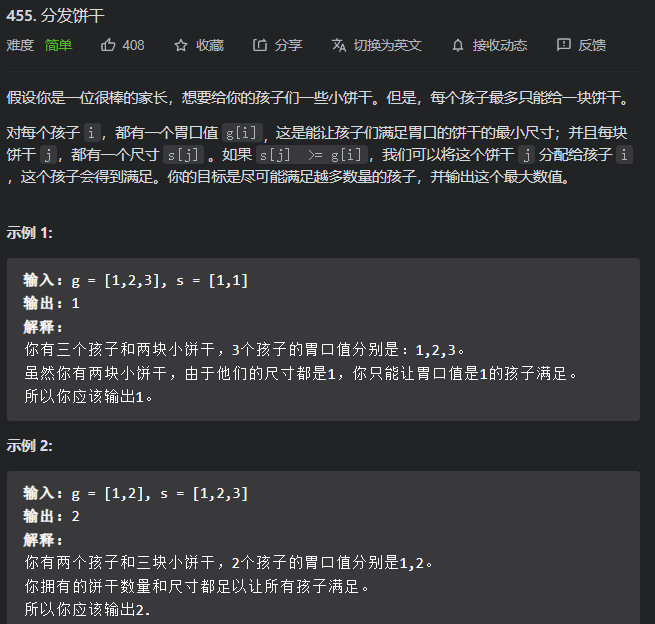
就是一个很简单的贪心题，想到方法就试试，万一过了呢?

class Solution {
public:
    int findContentChildren(vector<int>& g, vector<int>& s) {
        sort(g.begin(), g.end());
        sort(s.begin(), s.end());
        int ans = 0;
        int j = s.size() - 1;
        for(int i = g.size() - 1; i >= 0; i--){
            if(j >= 0 && s[j] >= g[i]) {
                ans++;
                j--;
            }
        }
        return ans;
    }
};

lc-day11

发表于 2021-11-23

859. 亲密字符串

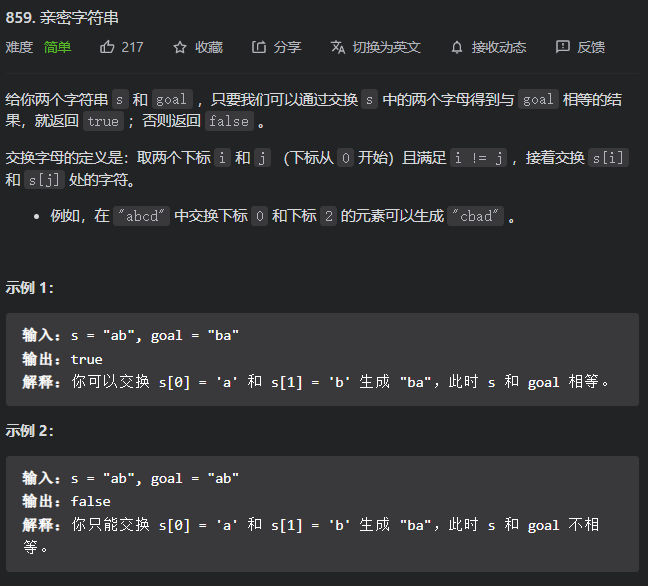
这个简单题写了一个多小时，纯纯恶心人的题，浪费时间

class Solution {
public:
    
    bool buddyStrings(string s, string goal) {
        if(s.size() != goal.size()) return false;
        vector<int> s1(26);
        vector<int> goal1(26);
        for(int i = 0; i < s.size(); i++){
            s1[s[i] - 'a']++;
            goal1[goal[i] - 'a']++;
        }
        int cnt = 0, flag = 0;
        for(int i = 0; i < s.size(); i++){
            if(s[i] != goal[i]) cnt++;
        }
        for(int i = 0; i < 26; i++) if(s1[i] > 1) flag = 1;
        if(s == goal && flag == 1) return true;
        if(s1 != goal1) return false;
        else{
            if(cnt == 2) return true;
        }
        return false;
        
        
    }
};

lc-day10

发表于 2021-11-22

654. 最大二叉树

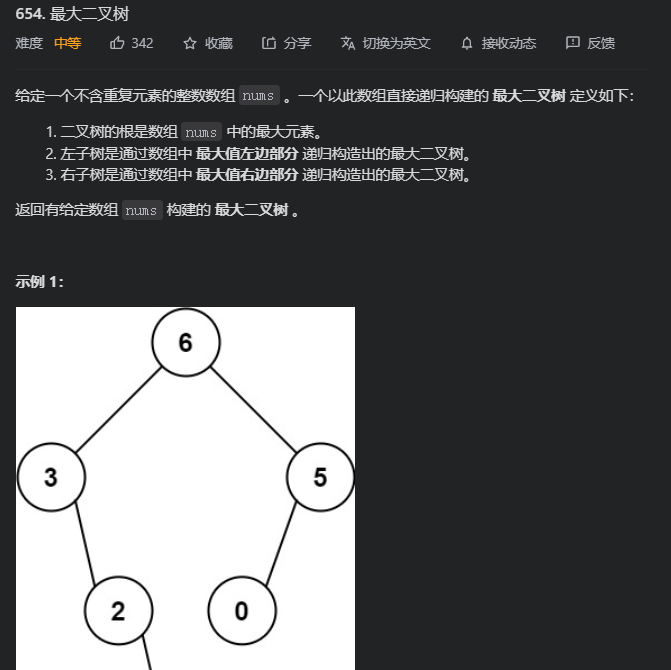
重刷了最大二叉树，发现两个有意思的点

如果递归变量数目不同，那就不能拿原函数直接递归，只能再写一个递归

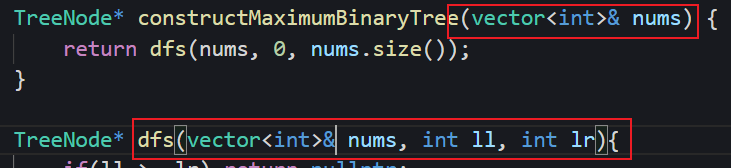
point 1

二叉树的边界构建一定要始终保持一致，开始是左闭右开那就一直左闭右开，开始是闭区间就一直是闭区间，这一点在归并、快速排序中很重要

point 2

上次借助Carl的代码写出来了，这次能手撕了

class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return dfs(nums, 0, nums.size());
    }

    TreeNode* dfs(vector<int>& nums, int ll, int lr){
        if(ll >= lr) return nullptr;
        int maxValue = -1, pos = 0;
        for(int i = ll; i < lr; i++) {
            if(maxValue < nums[i]){
                maxValue = nums[i];
                pos = i;
            }
        }
        TreeNode* node = new TreeNode(maxValue);
        node->left = dfs(nums, ll, pos);
        node->right = dfs(nums, pos + 1, lr);
        return node;

    }
};

为什么刷上面的题目呢？因为是为下面的题目做铺垫 ^_^

108. 将有序数组转换为二叉搜索树

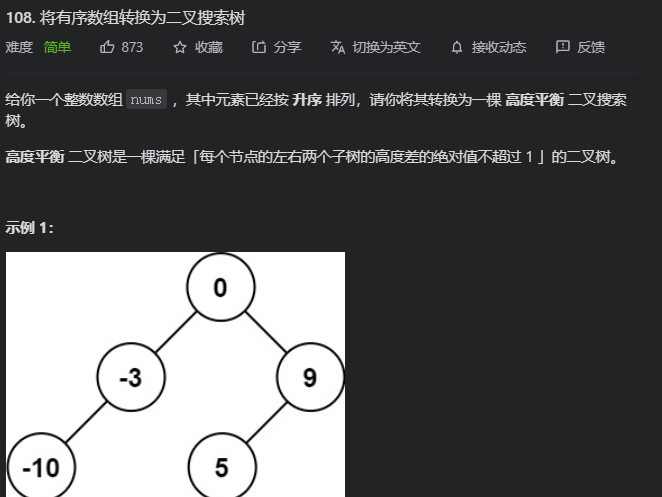
设好了区间后，直接用可以求pos了

实际上这题的pos包括了两种情况，一个表达式就能搞定

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return dfs(nums, 0, nums.size());
    }

    TreeNode* dfs(vector<int>& nums, int l, int r){
        if(l >= r) return nullptr;
        int pos = (l + r) / 2;
        TreeNode* node = new TreeNode(nums[pos]);
        node->left = dfs(nums, l, pos);
        node->right = dfs(nums, pos + 1, r);
        return node;
    }
};

再看看官方题解，区间设置也很有意思，它是左闭右闭区间

class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }

    TreeNode* helper(vector<int>& nums, int left, int right) {
        if (left > right) {
            return nullptr;
        }

        // 总是选择中间位置左边的数字作为根节点
        int mid = (left + right) / 2;

        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid - 1);
        root->right = helper(nums, mid + 1, right);
        return root;
    }
};

450.删除⼆叉搜索树中的节点

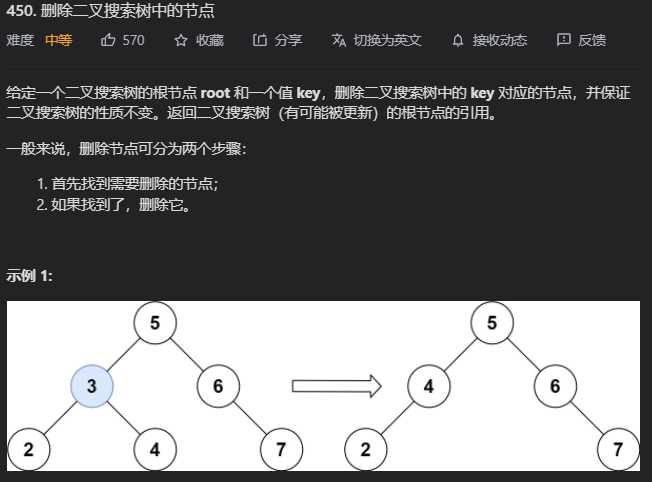
又是一个很久没写的题目，直接跪

class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(root == nullptr) return root;
        if(root->val == key){
            if(root->left == nullptr && root->right == nullptr) return nullptr;
            else if(root->left == nullptr) return root->right;
            else if(root->right == nullptr) return root->left;
            //第五种情况, 左右都不为空, root->val == key
            else {
                TreeNode* cur = root->right;//右子树
                while(cur->left != nullptr){
                    cur = cur->left;//最左结点, 是右子树最小值
                }
                cur->left = root->left;//把待删除点的左子树放在cur的左孩子上
                TreeNode* tmp = root;
                //将待删除点的右子树地址作为新root
                root = root->right;
                delete tmp;
                return root;
            }
        }
        if(root->val > key) root->left = deleteNode(root->left, key);
        if(root->val < key) root->right = deleteNode(root->right, key);
        return root;
    }
};

惊叹于别人函数设计的巧妙性，望尘莫及

538. 把二叉搜索树转换为累加树

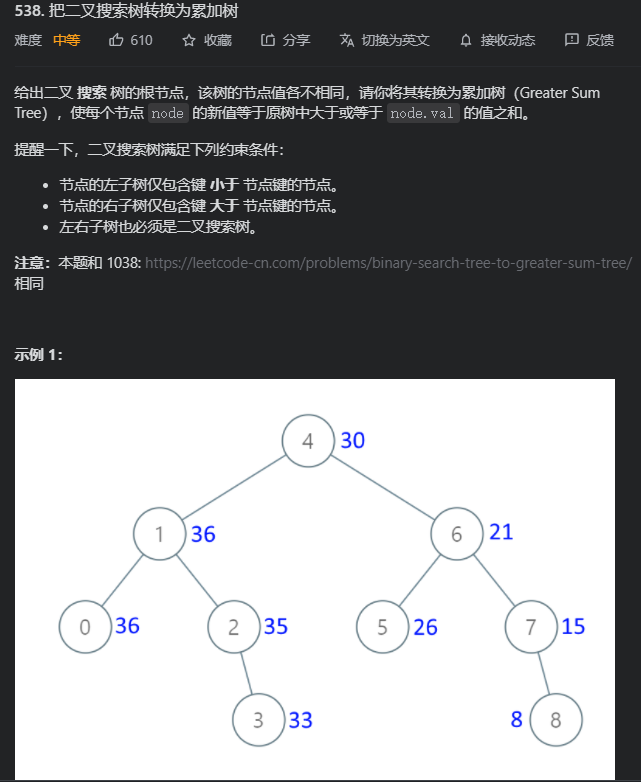
没写出来前觉得好难，经过卡尔的提示就很快写出来了。这题开始时觉得莫名其妙，为什么要这么累加，跟我想的完全不一样，结果没想到是反向累加，那就反向中序遍历就好了，顺便把之前的指针技巧给用上了

class Solution {
public:
    TreeNode* cur = nullptr;
    TreeNode* convertBST(TreeNode* root) {
        if(root == nullptr) return nullptr;
        convertBST(root->right);
        if(cur != nullptr) root->val += cur->val;
        cur = root;
        convertBST(root->left);
        return root;
    }
};

结束语

今天就把二叉树给收尾了，中间跳了一题不想写了，下次补上，下次见面二叉树应该是二周目了！我的定位暂时是前端，最终目标应该是sde，前端是一个快速入门的过渡阶段，