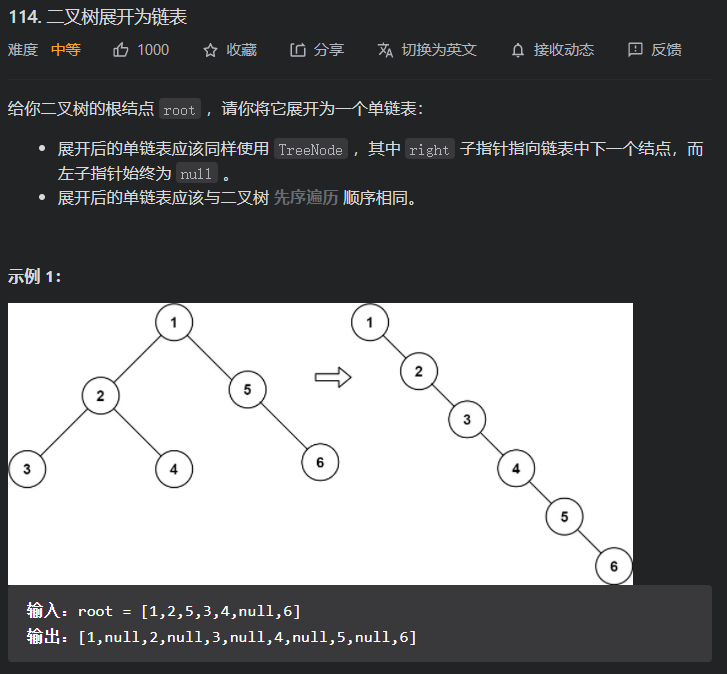
114. 二叉树展开为链表
1 | var flatten = function(root) { |
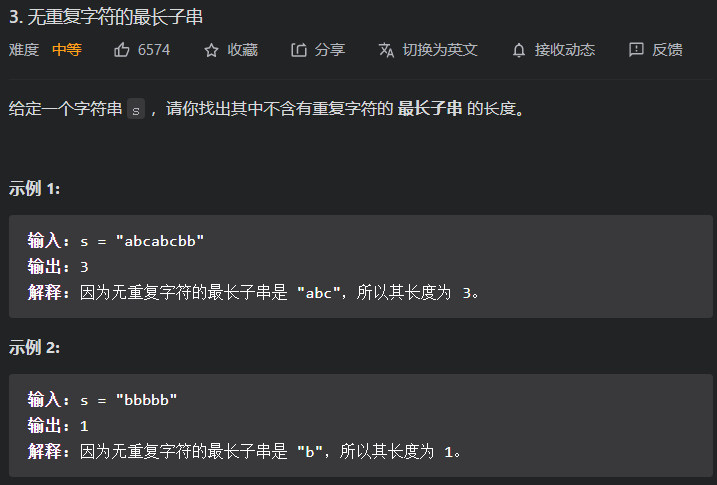
3. 无重复字符的最长子串
1 | /** |
使用最小花费爬楼梯
1 | /** |
一个简单题还做了半天, 没脸了
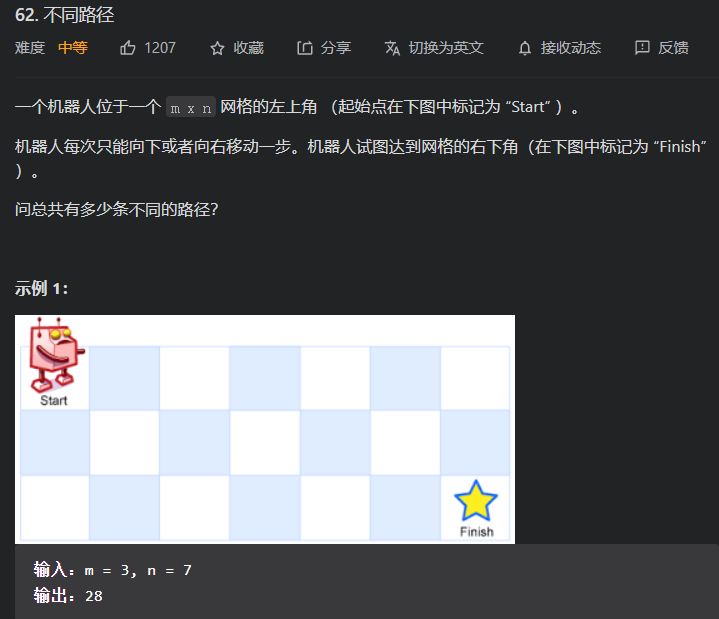
62. 不同路径
1 | /** |
我们发现数组每一次循环都可以重复利用上一次的
1 | /** |
记忆化搜索
1 | class Solution { |
Hydra blog

1 | var flatten = function(root) { |

1 | /** |
1 | /** |
一个简单题还做了半天, 没脸了

1 | /** |
我们发现数组每一次循环都可以重复利用上一次的
1 | /** |
记忆化搜索
1 | class Solution { |