激光炸弹

还卡我内存,一时代码还没过
学到了两个前缀和的运用技巧
关于初始化数组:可以将所有坐标+1,这样就回避了边界问题
前缀和问题可以节省一个数组,内存开销变小
边长r = x2 - x1 + 1, 如果题目给的是坐标, 那就是 x1 - 1 = x2 - r, 因为坐标x1是包括进矩形的,所以从x1 - 1开始,但这样也带来了一个问题, x1不能为0, 所以数组要从1开始计数
1 |
|
K倍区间

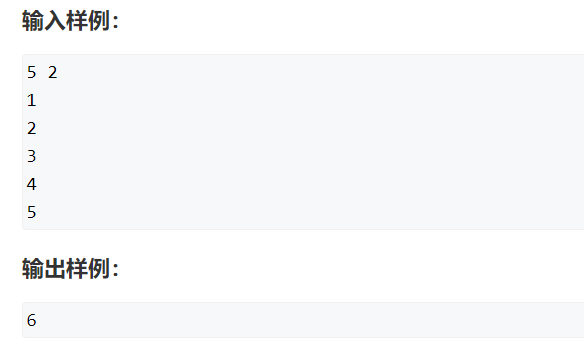
这题的方法太妙了,首先前缀和就不说了,直接上公式, s[R] - s[L - 1] % k == 0 ==> s[R] % k == s[L - 1] % k ,所以只要有两个数s[R] 和 s[L - 1]的前缀和mod k的余数相同,那么就必然是一个K倍区间,所以每次出现一个之前出现过的mod k的余数的数,就要res += cnt[之前出现过的余数], 而且还要出现次数加一
最后是一个边界问题,因为上面的都是两个端点所组成的区间(不包括左端点,所以是2~n的所有序列和子序列被包括了),有一种情况被排除了==>[0, n],所以一开始就要包括cnt[0]=1, 这个区间的第一个值为零,所以是一个万能区间(因为值为0,对余数无影响),只要有[1, n]的数符合情况,那它也就非零了
1 |
|
数的三次方根
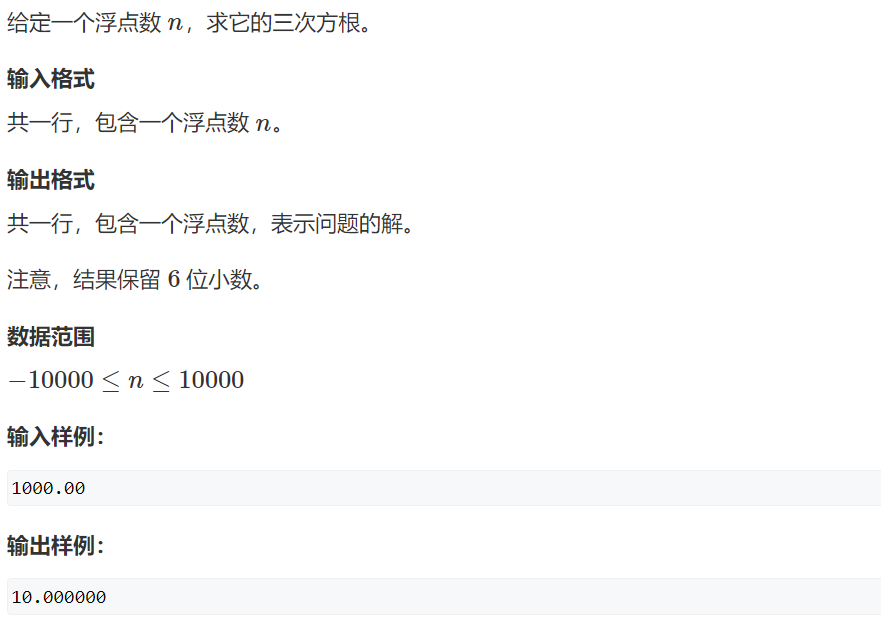
简单地二分
1 |
|