lc-day10

发表于

654. 最大二叉树

题目

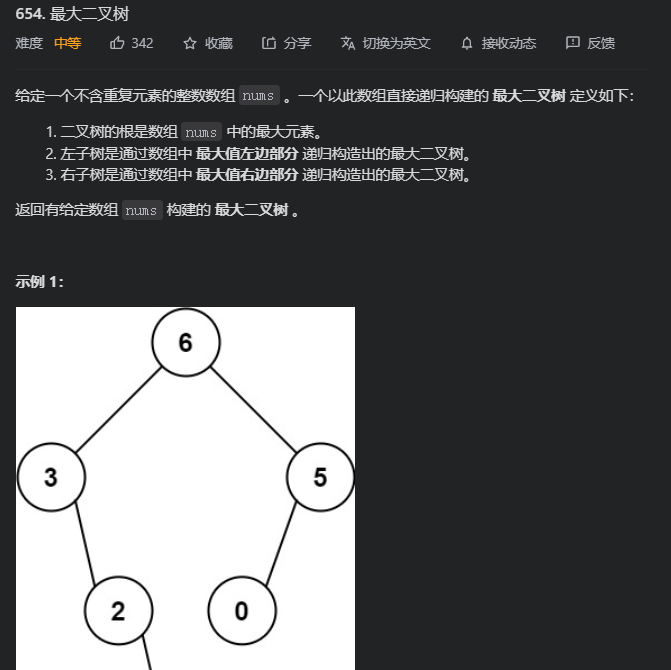
重刷了最大二叉树，发现两个有意思的点

如果递归变量数目不同，那就不能拿原函数直接递归，只能再写一个递归

point 1

二叉树的边界构建一定要始终保持一致，开始是左闭右开那就一直左闭右开，开始是闭区间就一直是闭区间，这一点在归并、快速排序中很重要

point 2

上次借助Carl的代码写出来了，这次能手撕了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return dfs(nums, 0, nums.size());
    }

    TreeNode* dfs(vector<int>& nums, int ll, int lr){
        if(ll >= lr) return nullptr;
        int maxValue = -1, pos = 0;
        for(int i = ll; i < lr; i++) {
            if(maxValue < nums[i]){
                maxValue = nums[i];
                pos = i;
            }
        }
        TreeNode* node = new TreeNode(maxValue);
        node->left = dfs(nums, ll, pos);
        node->right = dfs(nums, pos + 1, lr);
        return node;

    }
};

为什么刷上面的题目呢？ 因为是为下面的题目做铺垫 ^_^

108. 将有序数组转换为二叉搜索树

题目

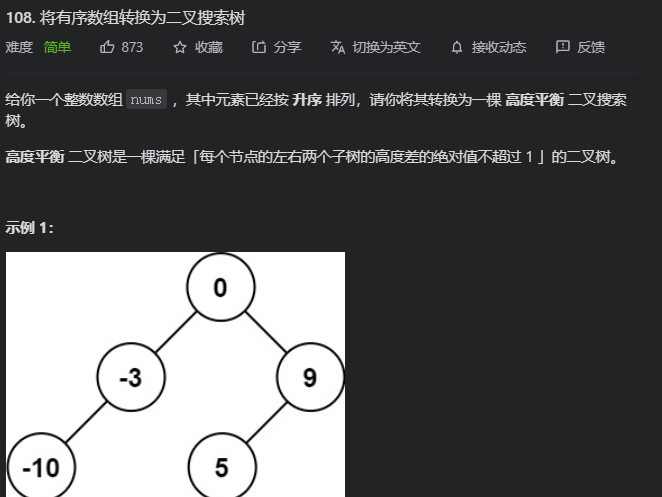
设好了区间后，直接用可以求pos了

实际上这题的pos包括了两种情况，一个表达式就能搞定

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return dfs(nums, 0, nums.size());
    }

    TreeNode* dfs(vector<int>& nums, int l, int r){
        if(l >= r) return nullptr;
        int pos = (l + r) / 2;
        TreeNode* node = new TreeNode(nums[pos]);
        node->left = dfs(nums, l, pos);
        node->right = dfs(nums, pos + 1, r);
        return node;
    }
};

再看看官方题解，区间设置也很有意思，它是左闭右闭区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        return helper(nums, 0, nums.size() - 1);
    }

    TreeNode* helper(vector<int>& nums, int left, int right) {
        if (left > right) {
            return nullptr;
        }

        // 总是选择中间位置左边的数字作为根节点
        int mid = (left + right) / 2;

        TreeNode* root = new TreeNode(nums[mid]);
        root->left = helper(nums, left, mid - 1);
        root->right = helper(nums, mid + 1, right);
        return root;
    }
};

450.删除⼆叉搜索树中的节点

题目

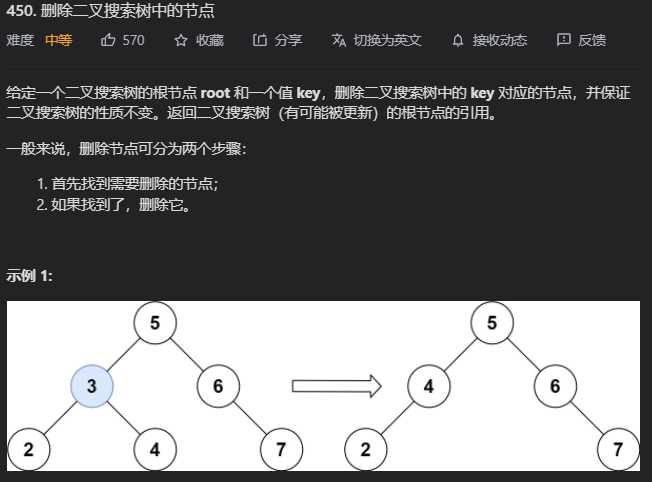
又是一个很久没写的题目，直接跪

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(root == nullptr) return root;
        if(root->val == key){
            if(root->left == nullptr && root->right == nullptr) return nullptr;
            else if(root->left == nullptr) return root->right;
            else if(root->right == nullptr) return root->left;
            //第五种情况, 左右都不为空, root->val == key
            else {
                TreeNode* cur = root->right;//右子树
                while(cur->left != nullptr){
                    cur = cur->left;//最左结点, 是右子树最小值
                }
                cur->left = root->left;//把待删除点的左子树放在cur的左孩子上
                TreeNode* tmp = root;
                //将待删除点的右子树地址作为新root
                root = root->right;
                delete tmp;
                return root;
            }
        }
        if(root->val > key) root->left = deleteNode(root->left, key);
        if(root->val < key) root->right = deleteNode(root->right, key);
        return root;
    }
};

惊叹于别人函数设计的巧妙性，望尘莫及

538. 把二叉搜索树转换为累加树

题目

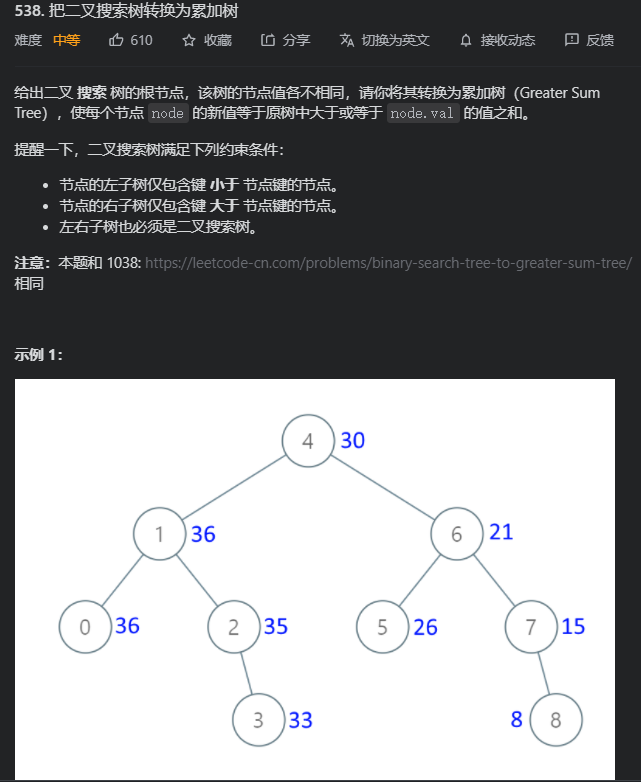
没写出来前觉得好难，经过卡尔的提示就很快写出来了。这题开始时觉得莫名其妙，为什么要这么累加，跟我想的完全不一样，结果没想到是反向累加，那就反向中序遍历就好了，顺便把之前的指针技巧给用上了

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    TreeNode* cur = nullptr;
    TreeNode* convertBST(TreeNode* root) {
        if(root == nullptr) return nullptr;
        convertBST(root->right);
        if(cur != nullptr) root->val += cur->val;
        cur = root;
        convertBST(root->left);
        return root;
    }
};

结束语

今天就把二叉树给收尾了，中间跳了一题不想写了，下次补上，下次见面二叉树应该是二周目了！我的定位暂时是前端，最终目标应该是sde，前端是一个快速入门的过渡阶段，