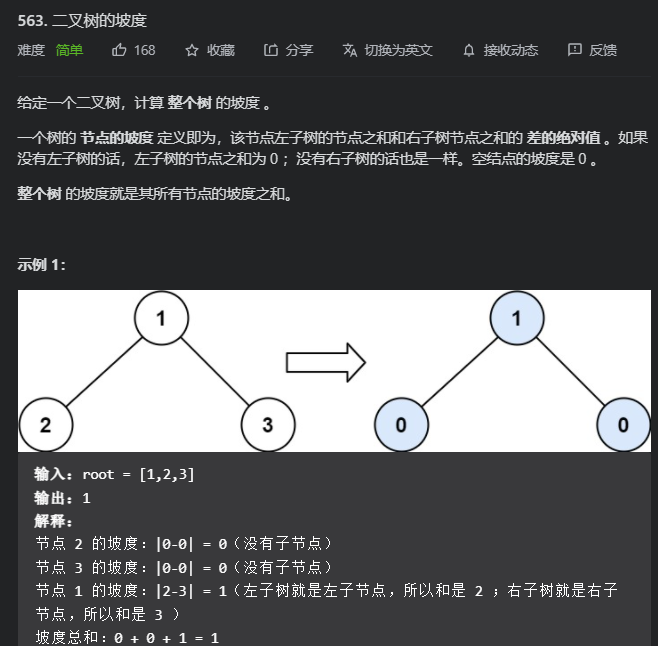
563. 二叉树的坡度
没想清除一个点,被卡了好久,二叉树的遍历别看只有短短几行代码,递归起来是真的要命,不好debug就很麻烦了,准备后期放假了玩命刷,现在就尽量把每题精刷一遍
1 | class Solution { |
没想清楚的是【递归返回值】,我错误地认为【返回值】能干同时干两件事:返回正确答案+能跑递归代码。实际上只能干一件事,就是跑代码。题目的答案则需要用一个ans另外计算
递归水太深,把握不住
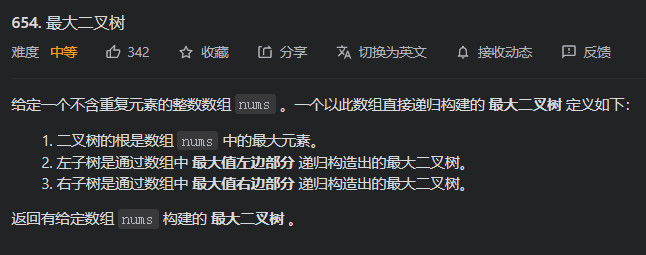
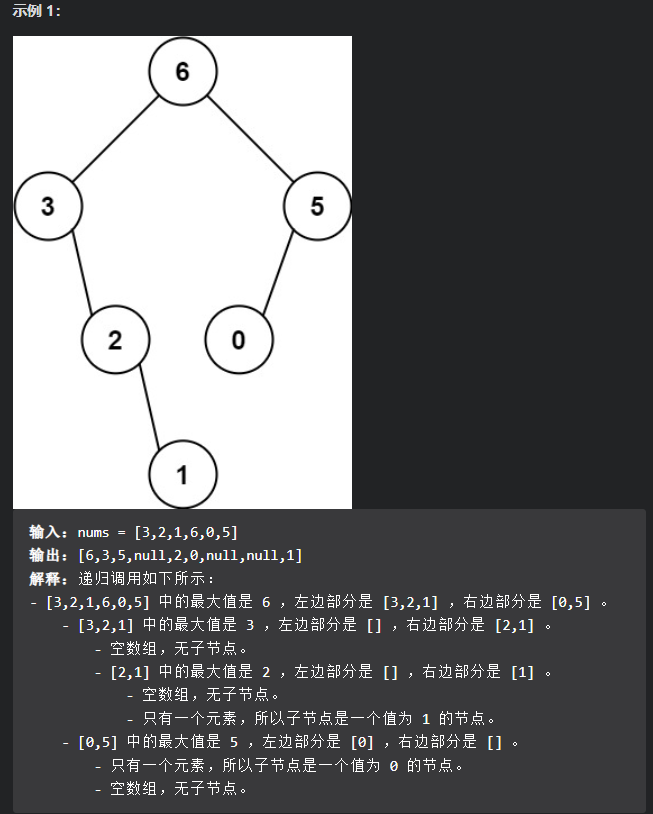
654.最大二叉树
构建二叉树只会写模板题,还要加强练习
1 | class Solution { |
简单暴力的写法,思路清晰,还学到一个技巧,动态数组还能这么玩
1 | class Solution { |
第二种方法把空节点引入到了递归中,所以省去了两个if条件
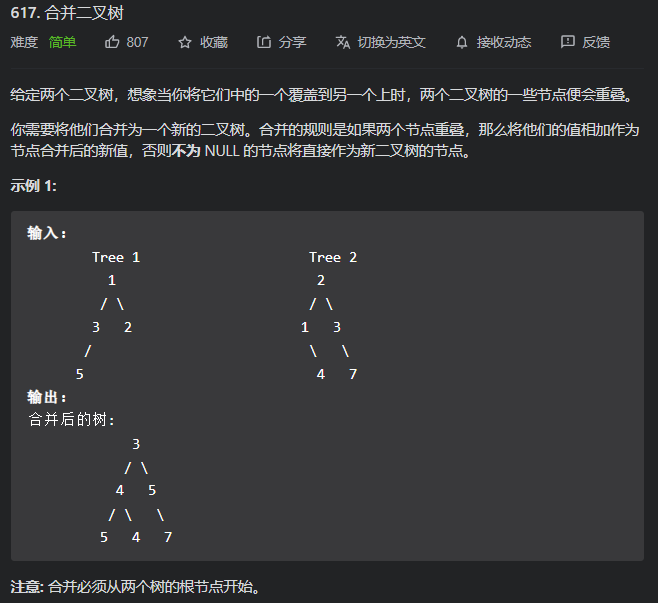
617. 合并二叉树
1 | class Solution { |
将root2树上的值移到root1树上就行了
700. 二叉搜索树中的搜索
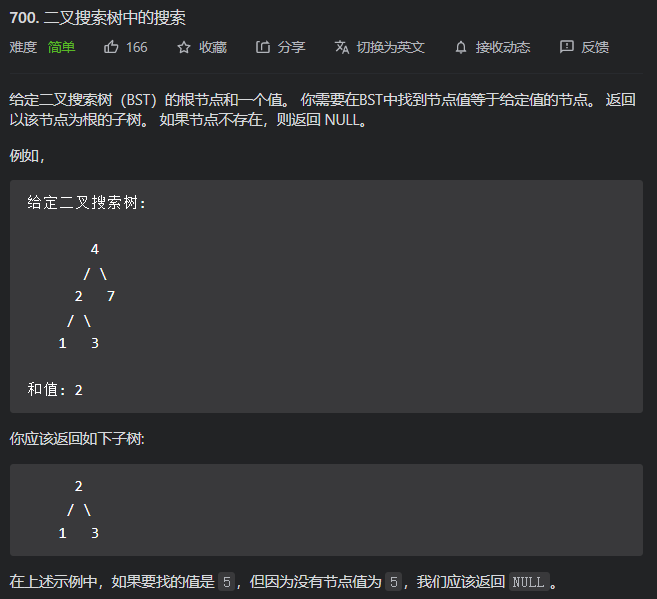
白给题
递归法
1 | class Solution { |
迭代法
1 | class Solution { |
98. 验证二叉搜索树
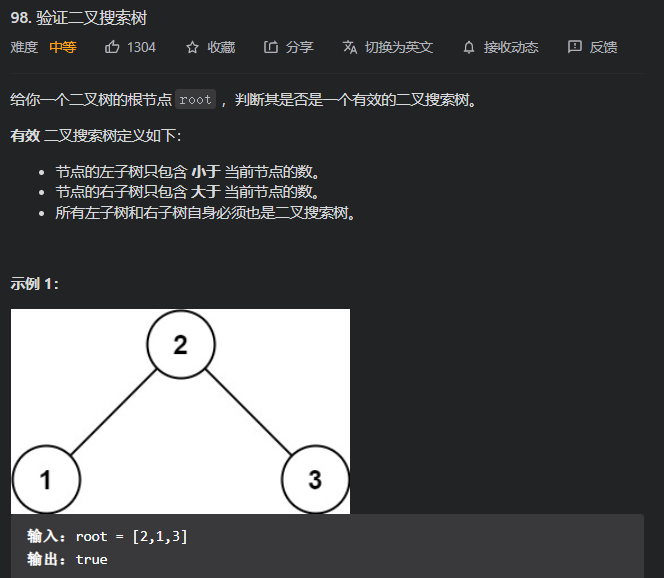
踩陷阱啦,我憨憨地用递归直接进行判断,左边val小右边val大,然后直接gg
正确思路应该是用中序遍历把它输出成数组,然后在数组里面判断是否是严格递增序列,不是判false
1 | class Solution { |
今天就到这吧